Instituto Brasileiro do Meio Ambiente e dos Recursos Naturais Renováveis
54
• Distribuição de abundância
(LogNormal)
–
este modelo objetiva descrever muitos conjun-
tos de dados de espécies com equações sim-
ples, cujos parâmetros possam ser utilizados
para a comparação de diferentes amostras de
espécies. Também usa modelos matemáticos
para inferir os processos que produzem a dis-
tribuição estudada (RICKLEFS, 2004).
May (1975) demonstrou que a distribuição
logNormal deveria ser encontrada em siste-
mas interativos com muitas espécies. Com
base nisso e nos artigos originais de Preston
(1980), desenvolveu-se a ideia de que o ajuste
à distribuição logNormal poderia ser um indi-
cativo de estabilidade (UGLAND; GRAY, 1982)
ou integridade biótica (KEVAN et al., 1997).
O modelo de logNormal ou de Preston corres-
ponde a uma distribuição de abundância de
diversas espécies na qual os logaritmos dos
efetivos repartem, de um lado e de outro, seu
valor médio, segundo a distribuição normal
(DAJOZ, 2005). Essa distribuição é encon-
trada em comunidades controladas por mui-
tos fatores ecológicos, que permitem a parti-
lha equilibrada dos recursos disponíveis, nas
quais existem poucas espécies com valores
de abundância extremos (raras e comuns) e a
maioria com valores de abundância intermediá-
rios (DAJOZ, 2005).
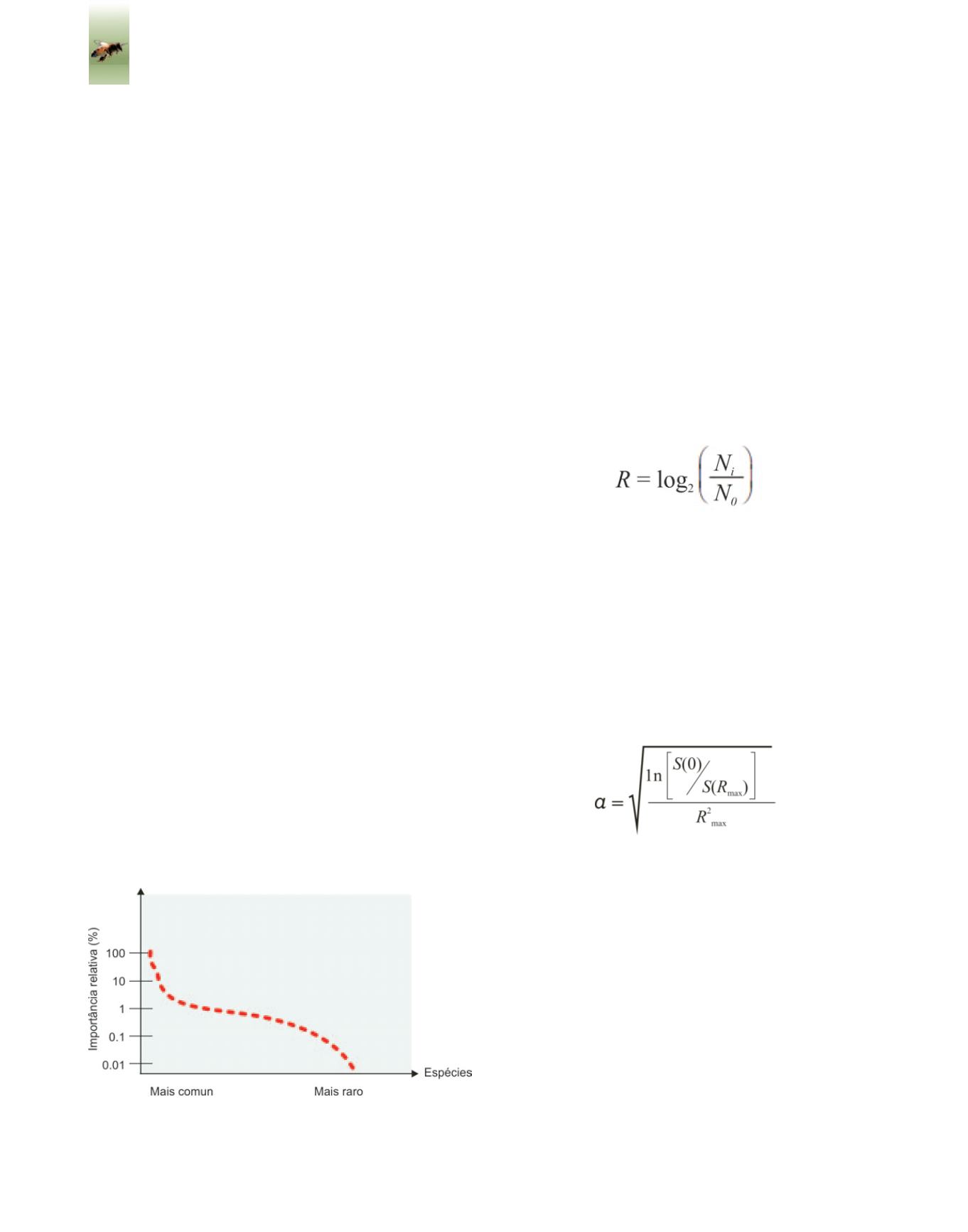
Para a análise do problema, rearranja-se as
frequências das espécies (Figura 30) pelo lo-
garitmo das classes de abundância usando o
logaritmo na base 2, de forma que cada clas-
se ou octavo represente o dobro do ranking da
classe de abundância anterior. Esse procedi-
mento é arbitrário, mas convencional em estu-
dos ecológicos (LUDWIG; REYNOLDS, 1988).
A distribuição logNormal é dada por:
O ajustamento de dados observados a uma cur-
va logNormal é realizado em três etapas:
(a)
Organização da distribuição das frequências ob-
servadas
Os dados observados são arranjados na forma
de uma distribuição de frequências, fornecendo o
número de espécies (idades) em cada classe de
abundância ou octavo. Seguindo a convenção de
Preston (1948), de expressar logaritmo de abundân-
cia na base 2, o
R
do
i-ésimo
octavo é dado por:
onde:
Ni
é a abundância de espécies no
i-ésimo
octavo;
N0
é a abundância de espécies no octavo modal.
(b)
Estimação dos parâmetros
A distribuição logNormal é completamente ca-
racterizada por dois parâmetros, S0 e
a
. Foi usado um
método simples para estimar valores para esses parâ-
metros, mas a regressão não linear poderia também ser
usada.
Uma aproximação para o parâmetro
a
é dado por:
Onde: S(0) é o número observado de espécie no octavo
modal,
S(R
max
)
é o número observado de espécies no octavo
“mais distante” da moda (indicado por
R
max
).
(c)
Verificação da bondade do ajustamento
Usando as estimativas para S0 e
a
, as frequên-
cias logNormal esperadas são computadas usando a
equação 4.1, e o teste de bondade de ajustamento do
modelo para as frequências observadas é “testado”
com uma estatística qui-quadrado.
Os graus de liberdade são iguais ao número de
octavos menos 2. Uma vez que se está apenas tentando
obter umajuste aproximado, essa estatística qui-quadra-
da deve ser usada como um guia para a seleção de pa-
râmetros, mais do que como um teste estatístico formal.
(-a
2
R
2
)
S(R) =
S
0
e
Figura 30
. Distribuição do ranking das espécies por sua im-
portância relativa.


